Little Z raised a question: 
Given a string S of length n containing only lowercase letters. 
You need to select several non-empty substrings of S so that they are disjoint pairwise, and each substring is a palindrome. 
Assuming you have selected K substrings(s₁, s₂...s_k) that satisfy the above conditions, your score is the sum of the lengths of all substrings minus K. It is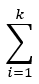 len(s_i) − K But Little Z is a dedicated person, and to increase difficulty, Little Z requires that each palindrome string contain at most one kind of letter 
Little Z wants you to find the maximum score. 

A positive integer T in the first line represents the number of test groups, for each group of test data: The only line contains a string of length n which containing only lowercase letters. T ≤ 20, ∑n ≤ 10⁶

For each test data, print a number representing the maximum score

In the first case, Only one palindromic substring "bbb" exists, get $K$ = 1, $\sum_{i=1}^{K}$ $len (s_i)$  = 3 , so $\sum_{i=1}^{K} len(s_i)  - K$ = 2

 2023“钉耙编程”中国大学生算法设计超级联赛（2）